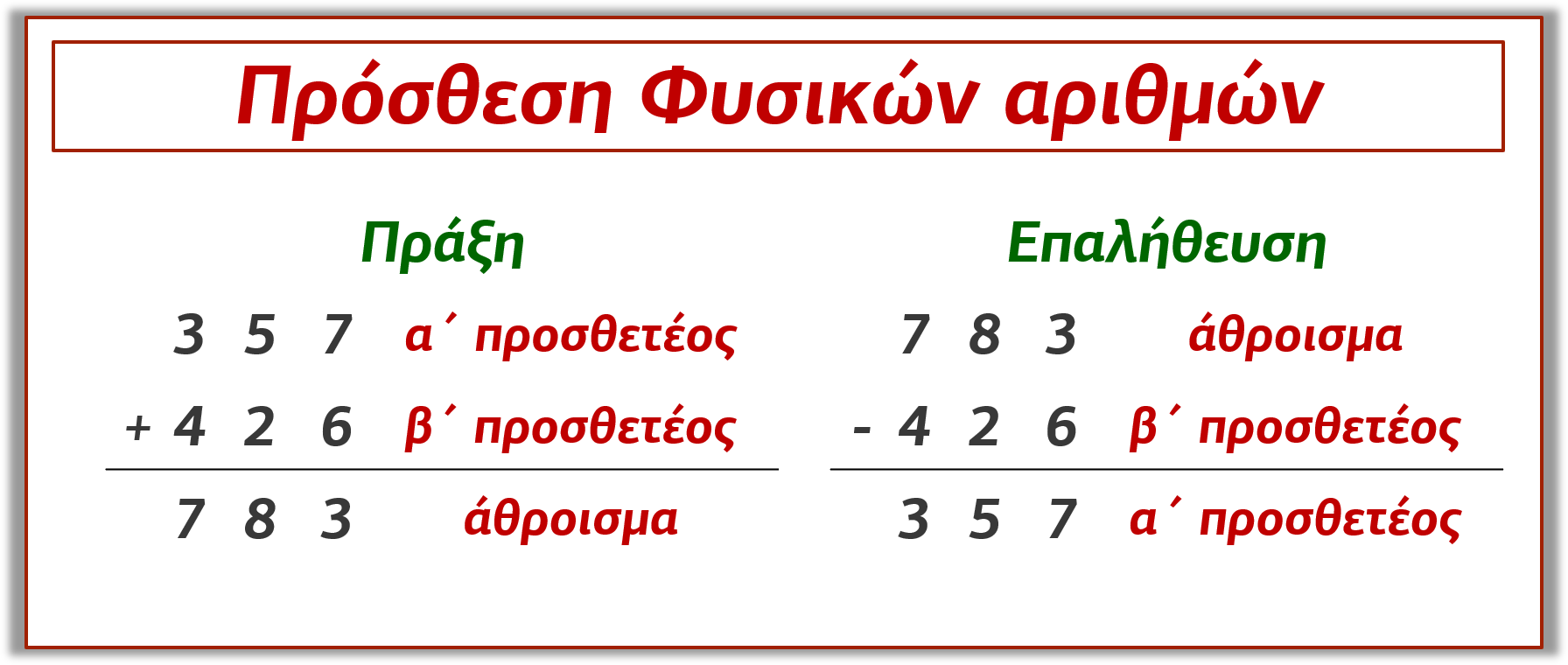
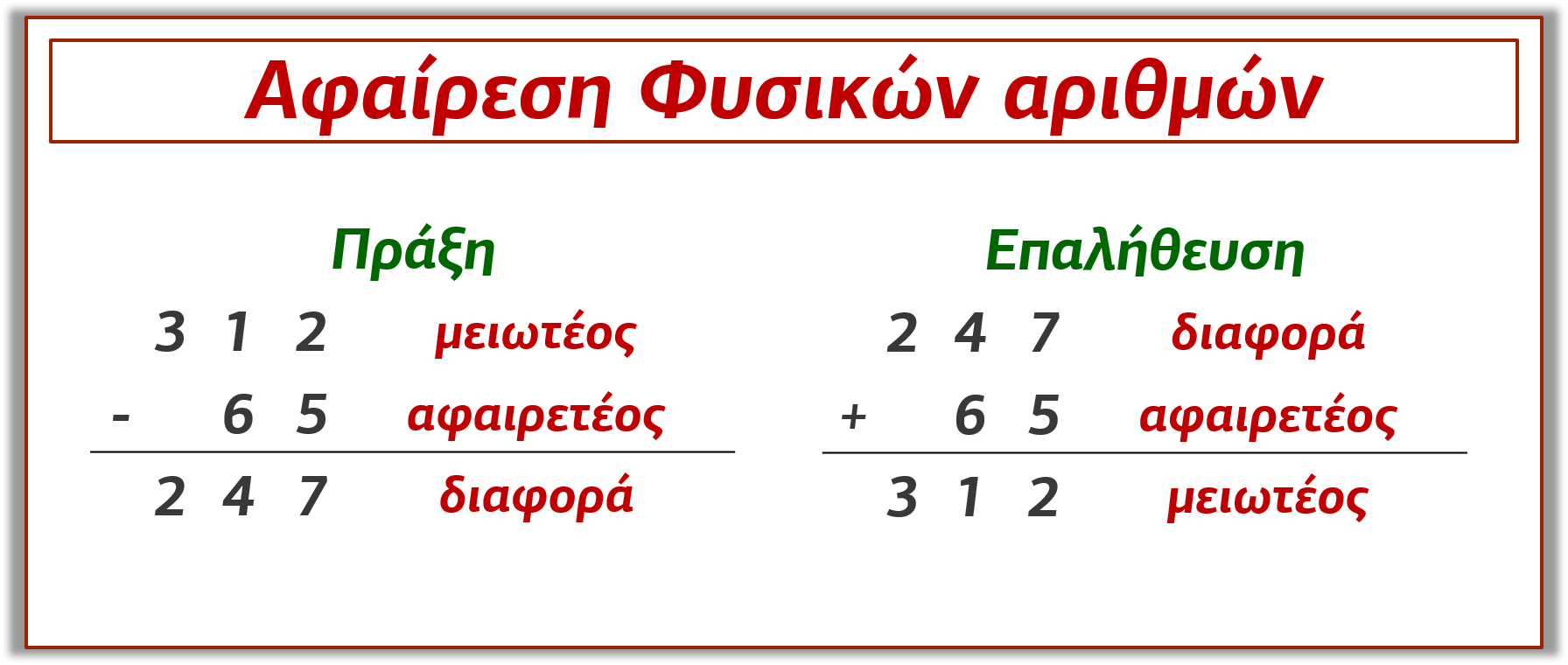
Θεωρία

Θεωρία

Ο Πυθαγόρας και ο Πυθαγόρειος πίνακας

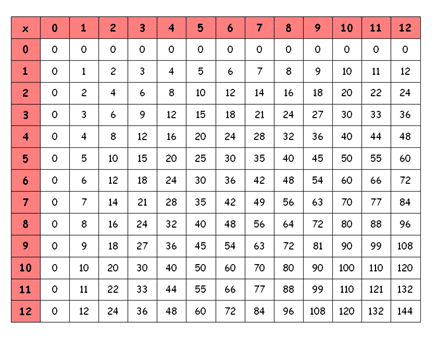Ο Πυθαγόρας ο Σάμιος, ο μεγάλος Έλληνας φιλόσοφος και μαθηματικός, που γεννήθηκε στη Σάμο το 580 π.Χ., ίδρυσε την περίφημη Πυθαγόρειο Φιλοσοφική Σχολή. Είναι ο κατεξοχήν θεμελιωτής των ελληνικών μαθηματικών. Με τις μελέτες του βοήθησε στην ανάπτυξη των Μαθηματικών και ιδιαίτερα της Γεωμετρίας. Λέγεται ότι ήταν ο άνθρωπος που έβλεπε παντού αριθμούς.

Ο διπλανός πίνακας είναι επινόηση του Πυθαγόρα για να δείξει πώς υπολογίζονται τα γινόμενα του πολλαπλασιασμού των φυσικών αριθμών οι οποίοι έως τότε γίνονταν με το μυαλό ή απλούστερα με πετραδάκια.

Φαίνεται κάτι απλό! Ωστόσο, ο Πυθαγόρας αφιέρωσε είκοσι ολόκληρα χρόνια της ζωής του, ώσπου να επινοήσει αυτόν τον πίνακα, ο οποίος έκανε αθάνατο το όνομά του στους κατοπινούς αιώνες.

Πολλαπλασιασμός

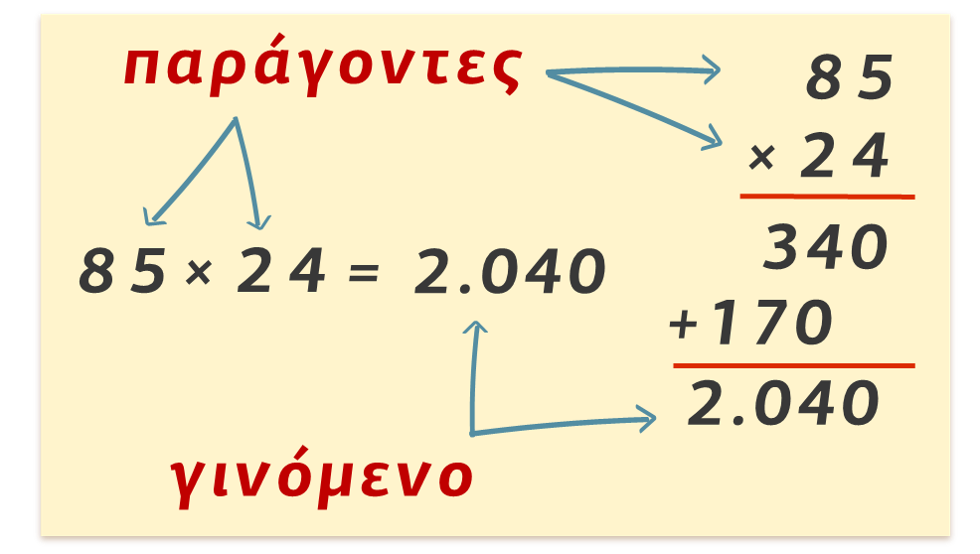Πολλαπλασιασμός είναι η πράξη με την οποία από δύο φυσικούς αριθμούς βρίσκουμε έναν τρίτο φυσικό αριθμό, ο οποίος λέγεται γινόμενο των αριθμών αυτών.

Οι αριθμοί οι οποίοι πολλαπλασιάζονται λέγονται παράγοντες του γινομένου.

π.χ.  5 × 8 = 40

Θεωρία

Πολλαπλάσιο (Π) ενός φυσικού αριθμού λέγεται ο αριθμός που προκύπτει όταν τον πολλαπλασιάσουμε με έναν άλλο φυσικό αριθμό (0, 1, 2, 3, 4, 5, . . .)

Παράδειγμα

Τα πολλαπλάσια του 2 και του 3

Π2 = 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, …

Π3 = 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …

Κάθε φυσικός αριθμός έχει άπειρα πολλαπλάσια γιατί είναι και άπειροι οι αριθμοί με τους οποίους μπορώ να τον πολλαπλασιάσω

3 τρόποι για να βρίσκω το Ελάχιστο Κοινό Πολλαπλάσιο

3 τρόποι για να βρίσκω τον Μέγιστο Κοινό Διαιρέτη

Θεωρία

Θεωρία

Διαίρεση είναι η πράξη με την οποία χωρίζουμε – μοιράζουμε έναν αριθμό σε ίσα μέρη, τόσα όσα μας λέει ένας άλλος αριθμός.

Κάνουμε διαίρεση όταν θέλουμε να μοιράσουμε (διαίρεση μερισμού) ή όταν θέλουμε να μετρήσουμε (διαίρεση μέτρησης).

  • Διαίρεση μερισμού. Όταν ξέρουμε την τιμή των πολλών μονάδων και ζητάμε να βρούμε την τιμή της μιας μονάδας ( μοιράζω ένα ποσό σε ίσα μέρη)

π.χ. Τα 5 βάζα με μέλι ζυγίζουν 10 κιλά. Πόσο ζυγίζει το ένα.

  • Διαίρεση μέτρησης. Όταν ξέρουμε την τιμή των πολλών μονάδων, ξέρουμε και την τιμή της μιας μονάδας και ζητάμε να βρούμε πόσες είναι οι μονάδες (Θέλω να δω πόσες φορές χωράει μια ποσότητα σε μία άλλη)

π.χ. Έχω ένα δοχείο με 10 κιλά μέλι. γέμισα βαζάκια των 2 κιλών. Πόσα βαζάκια γέμισα;

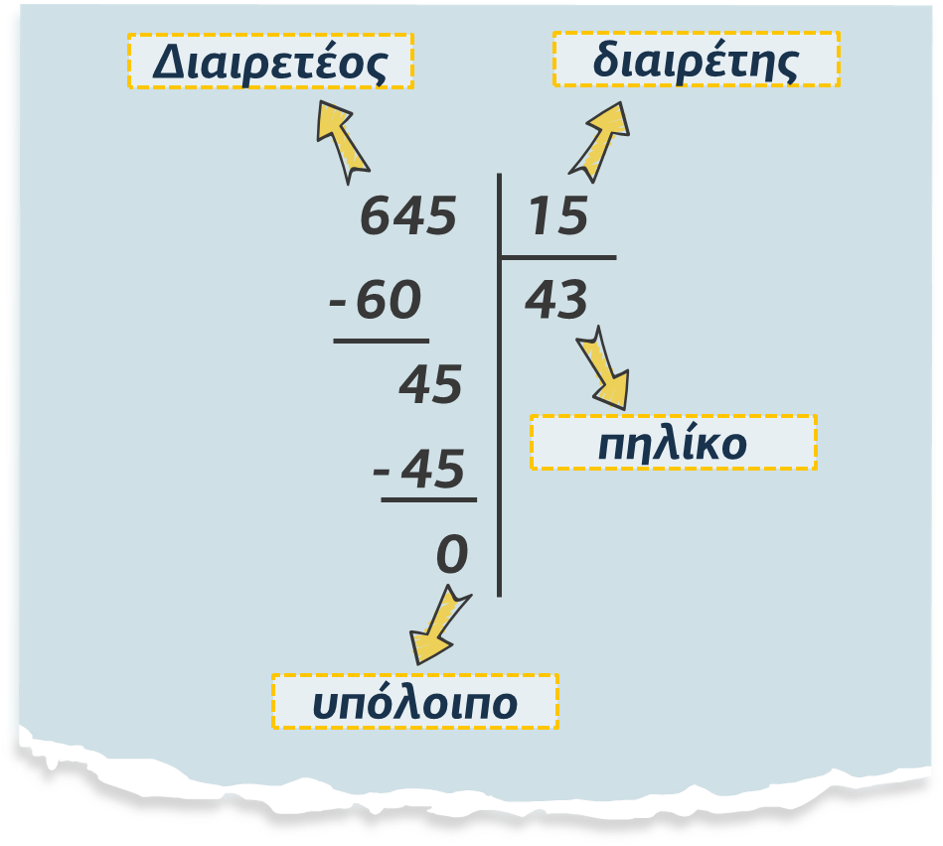Με την πράξη της διαίρεσης έχουμε δύο φυσικούς αριθμούς Δ (Διαιρετέο) και δ (διαιρέτη) και βρίσκουμε δύο άλλους φυσικούς αριθμούς π (πηλίκο) και υ (υπόλοιπο), έτσι ώστε να ισχύει:

Δ = δ • π + υ

  • Το υπόλοιπο είναι πάντα αριθμός μικρότερος από τον διαιρέτη και μεγαλύτερος ή ίσος του μηδενός.
  • Αν το υπόλοιπο υ είναι 0, τότε έχουμε μία Τέλεια Διαίρεση: Δ = δ • π
  • Η διαίρεση της μορφής Δ = δ • π + υ λέγεται Ευκλείδεια Διαίρεση.
Scroll to top