-
Αριθμοί και πράξεις
Σε αυτή τη θεματική ενότητα θα ασχοληθούμε με τους αριθμούς και τις πράξεις με αριθμούς.
Θα ξεκινήσουμε από τα αριθμητικά σύμβολα τα οποία χρησιμοποιούμε από την Α΄ Δημοτικού για να φτιάξουμε τους αριθμούς και να κάνουμε υπολογισμούς.
Ξέρετε πως οι Ινδοί τα χρησιμοποιούσαν από το 350 π.X.; Γνωρίζετε ακόμα ότι τα δίδαξαν αργότερα οι Άραβες στους Ευρωπαίους και για τον λόγο αυτό ονομάστηκαν «αραβικοί αριθμοί»;
Τα σύμβολα που γνωρίζουμε δεν τελειοποιήθηκαν σε κάποιον ορισμένο χρόνο ή τόπο αλλά εξελίχτηκαν με συνεχή ανάπτυξη και πιθανότατα τελειοποιήθηκαν τους τελευταίους αιώνες.
Στο σκίτσο που ακολουθεί βλέπετε την εξέλιξη των συμβόλων από το 800 μετά Χριστόν έως σήμερα.
Τι θα μάθουμε σε αυτή την ενότητα:
1. Φυσικοί αριθμοί
2. Δεκαδικοί αριθμοί
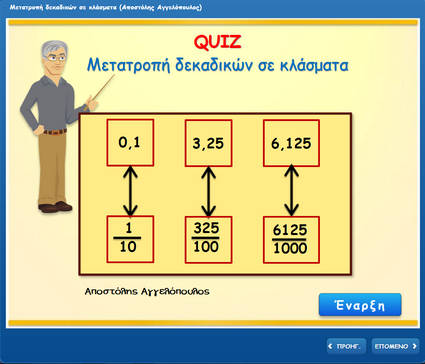
3. Μετατροπή δεκαδικών σε κλάσματα και αντίστροφα
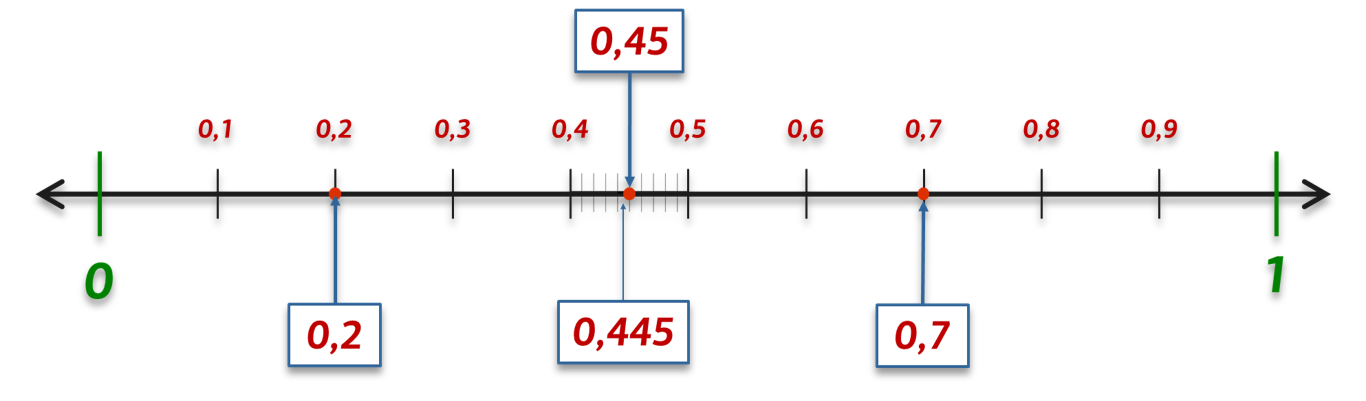
4. Σύγκριση φυσικών ή δεκαδικών αριθμών
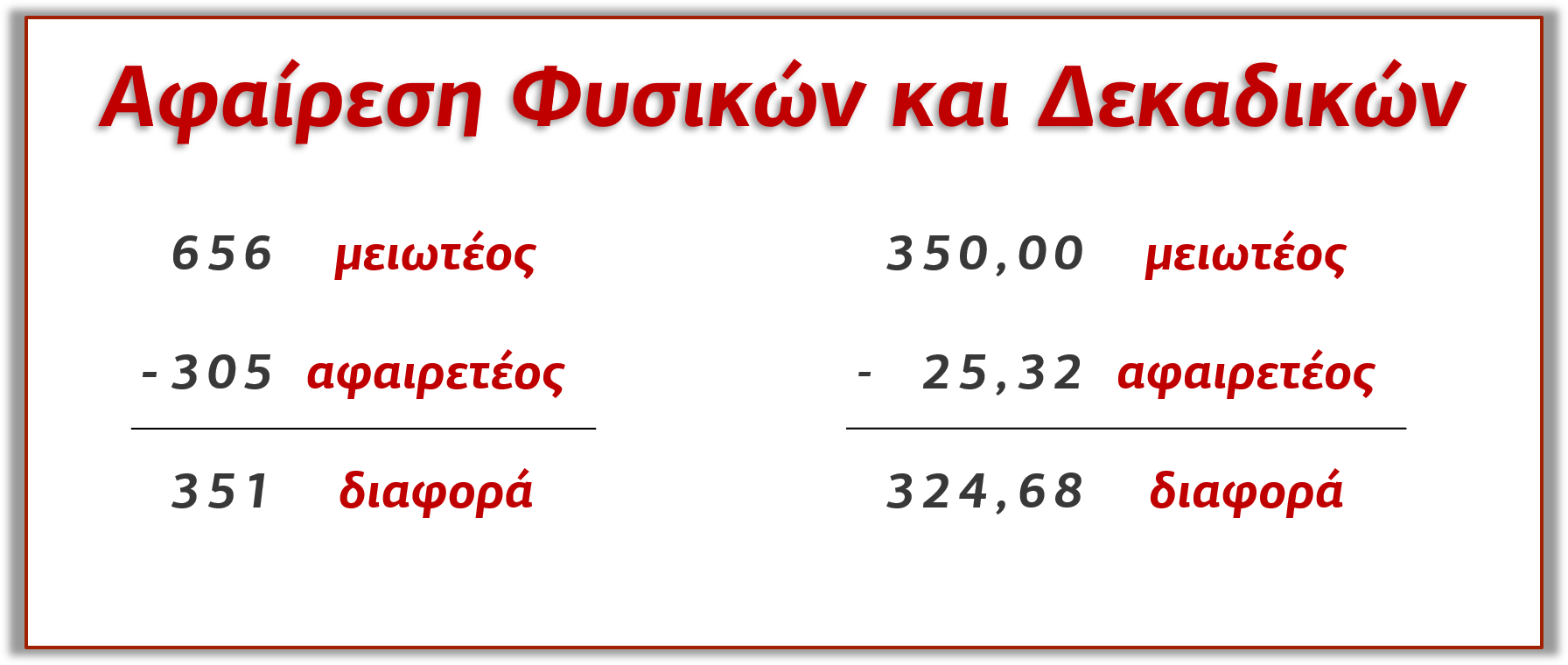
5. Πρόσθεση και αφαίρεση φυσικών και δεκαδικών αριθμών
6. Πολλαπλασιασμός φυσικών και δεκαδικών αριθμών
7. Διαίρεση φυσικών και δεκαδικών αριθμών
8. Πράξεις με μεικτές αριθμητικές παραστάσεις
11. Στρογγυλοποίηση φυσικών και δεκαδικών αριθμών
12. Διαιρέτες ενός αριθμού - Μ.Κ.Δ. αριθμών
13. Κριτήρια διαιρετότητας
Θεωρία
Φυσικοί αριθμοί λέγονται οι αριθμοί που βρίσκονται καθημερινά στη φύση, γύρω μας.
π.χ. 1 μήλο. 2 παιδιά. 5 αυτοκίνητα. 100 πρόβατα. 1.000 δέντρα κλπ.
Εκτός από πλήθος οι αριθμοί αυτοί μπορούν να δηλώσουν και τη θέση - σειρά που μπορεί να βρίσκεται κάποιος -οια, την τιμή μεγέθους, κώδικα επικοινωνίας.
π.χ. στη σειρά είναι 2ος. Κάθομαι στο 3ο θρανίο. Πηγαίνω στο 11ο Δ.Σ. κλπ.
Κάθε φυσικός αριθμός έχει έναν επόμενο και έναν προηγούμενο φυσικό αριθμό, εκτός από το 0 που έχει μόνο επόμενο, το 1.
Οι φυσικοί αριθμοί χωρίζονται σε δύο κατηγορίες :
Τους άρτιους ή ζυγούς, που είναι οι φυσικοί αριθμοί που διαιρούνται με το 2.
Τους περιττούς ή μονούς, που είναι οι φυσικοί αριθμοί που δε διαιρούνται με το 2.
Χρησιμοποιώντας μόνο τα δέκα γνωστά ψηφία, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, το δεκαδικό σύστημα αρίθμησης μας δίνει την δυνατότητα να σχηματίσουμε άπειρο (αμέτρητο ) πλήθος αριθμών.
Θεωρία
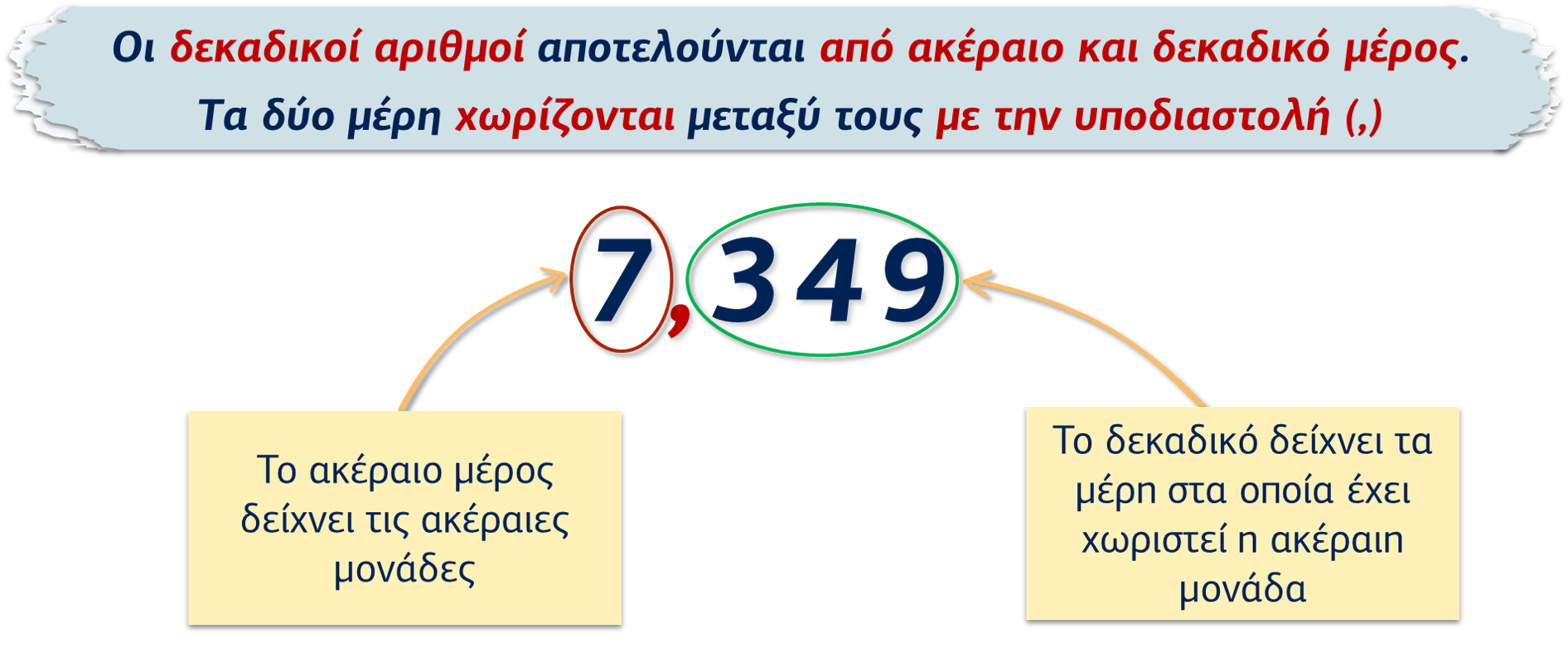
Όταν στην καθημερινή ζωή θέλουμε να εκφράσουμε ένα μέγεθος με ακρίβεια, τότε χρησιμοποιούμε τους δεκαδικούς αριθμούς. Οι αριθμοί αυτοί περιέχουν το ακέραιο μέρος ενός αριθμού και το δεκαδικό μέρος του. Ο χωρισμός ακέραιου και δεκαδικού μέρους γίνεται με την υποδιαστολή (κόμμα).
π.χ. Το παιδί έχει ύψος που 1,38 μ.
Στο ακέραιο μέρος, τα ψηφία ανάλογα με τη θέση τους μπορεί να δηλώνουν Μονάδες (Μ), Δεκάδες (Δ), Εκατοντάδες (Ε)
Στο δεκαδικό μέρος τα ψηφία μπορεί να δηλώνουν δέκατα (δεκ.), εκατοστά (εκ.), χιλιοστά (χιλ.)
Η αξία ενός δεκαδικού αριθμού δεν αλλάζει αν προσθέσουμε ή διαγράψουμε μηδενικά από το τέλος του δεκαδικού αριθμού
Θεωρία
Δεκαδικά κλάσματα είναι τα κλάσματα που έχουν παρονομαστή το 10 ή το 100 ή το 1000…
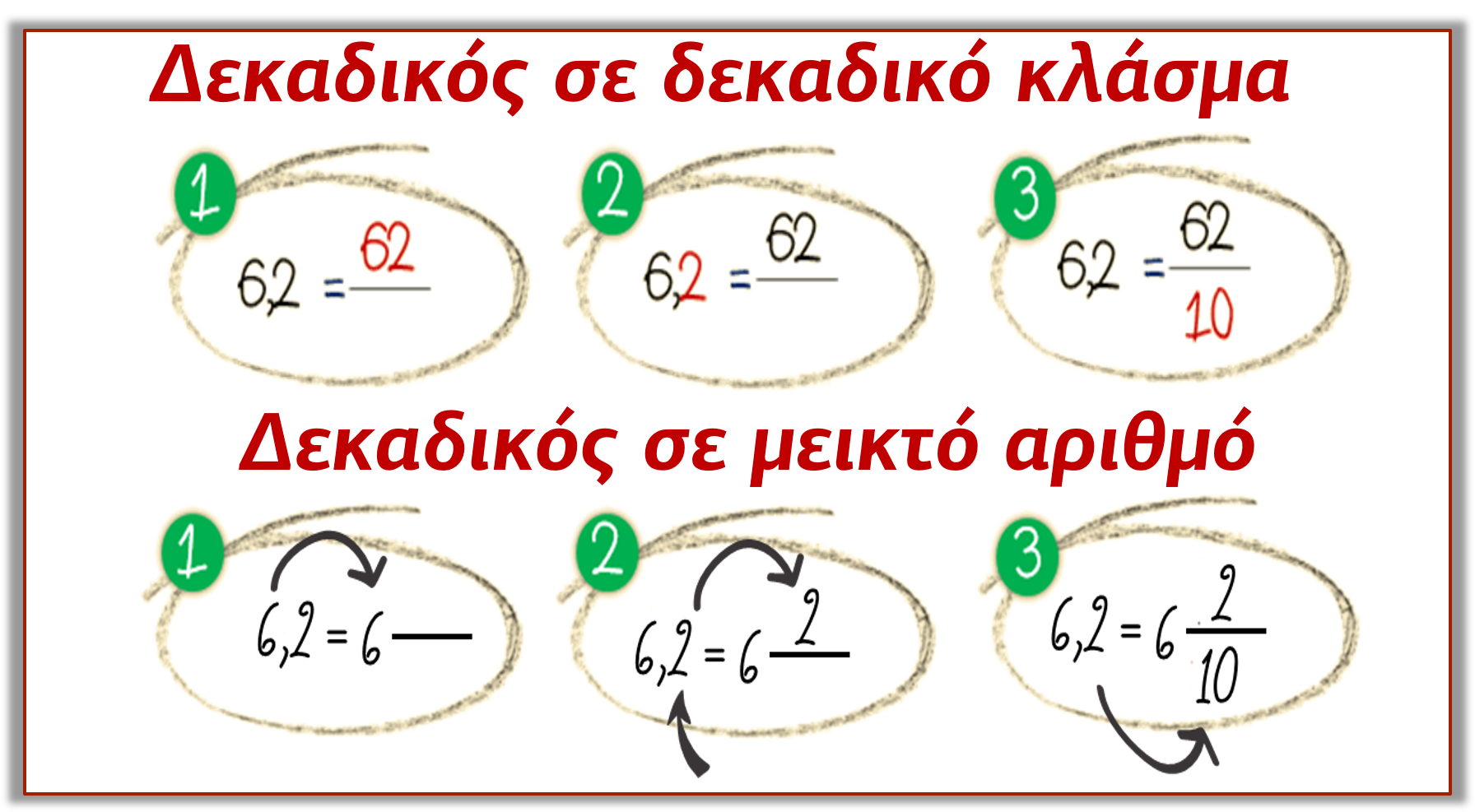
Οι δεκαδικοί αριθμοί μπορούν να γραφτούν και σαν δεκαδικά κλάσματα και αντιστρόφως.
1. Γράφουμε στον αριθμητή τον δεκαδικό αριθμό χωρίς την υποδιαστολή.
2. Μετράμε τα ψηφία του δεκαδικού μέρους.
3. Γράφουμε στον παρονομαστή το 1 και πίσω από το 1, τόσα μηδενικά όσα και τα ψηφία που μετρήσαμε.
1. Γράφουμε στον αριθμητή τα δεκαδικά ψηφία
2. Το ακέραιο μέρος του δεκαδικού γράφεται ως ακέραιος του μεικτού.
3. Γράφουμε στον παρονομαστή το 1 και πίσω από το 1, τόσα μηδενικά όσα και τα ψηφία του δεκαδικού μέρους του δεκαδικού μας αριθμού.
1. Γράφουμε τον αριθμητή όπως τον βλέπουμε δίπλα στο κλάσμα.
2. Μετράμε τα μηδενικά του παρονομαστή.
3. Μετράμε τόσες θέσεις ψηφίων όσα και τα μηδενικά.
4. Βάζουμε υποδιαστολή αριστερά του ψηφίου.
Θεωρία
Θεωρία
Ο Πυθαγόρας και ο Πυθαγόρειος πίνακας
Ο Πυθαγόρας ο Σάμιος, ο μεγάλος Έλληνας φιλόσοφος και μαθηματικός, που γεννήθηκε στη Σάμο το 580 π.Χ., ίδρυσε την περίφημη Πυθαγόρειο Φιλοσοφική Σχολή. Είναι ο κατεξοχήν θεμελιωτής των ελληνικών μαθηματικών. Με τις μελέτες του βοήθησε στην ανάπτυξη των Μαθηματικών και ιδιαίτερα της Γεωμετρίας. Λέγεται ότι ήταν ο άνθρωπος που έβλεπε παντού αριθμούς.
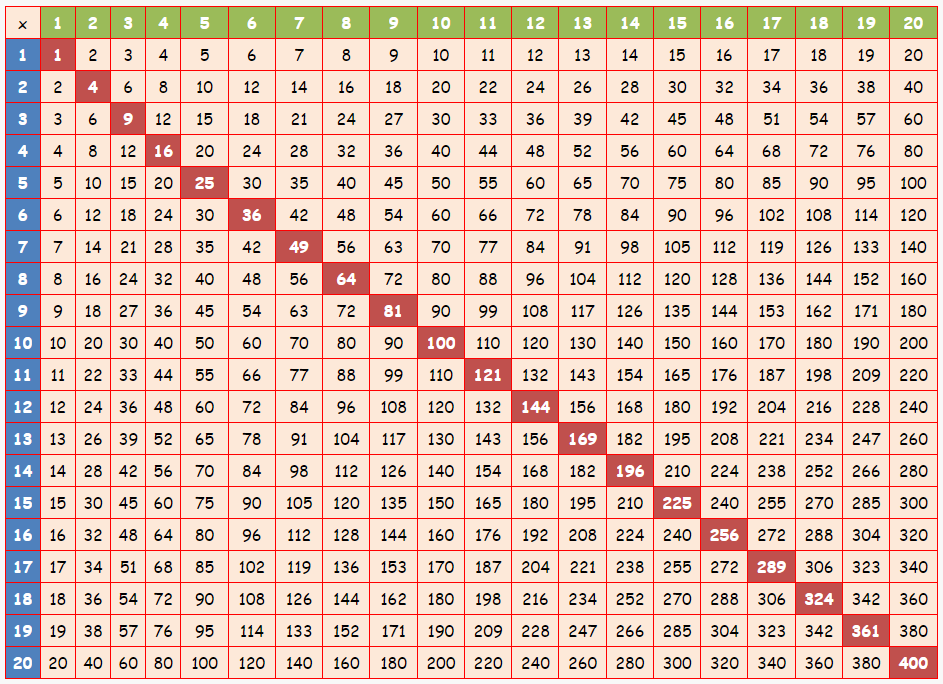
Ο διπλανός πίνακας είναι επινόηση του Πυθαγόρα για να δείξει πώς υπολογίζονται τα γινόμενα του πολλαπλασιασμού των φυσικών αριθμών οι οποίοι έως τότε γίνονταν με το μυαλό ή απλούστερα με πετραδάκια.
Φαίνεται κάτι απλό! Ωστόσο, ο Πυθαγόρας αφιέρωσε είκοσι ολόκληρα χρόνια της ζωής του, ώσπου να επινοήσει αυτόν τον πίνακα, ο οποίος έκανε αθάνατο το όνομά του στους κατοπινούς αιώνες.
Πολλαπλασιασμός και ιδιότητες του
Πολλαπλασιασμός είναι η πράξη με την οποία από δύο φυσικούς αριθμούς βρίσκουμε έναν τρίτο φυσικό αριθμό, ο οποίος λέγεται γινόμενο των αριθμών αυτών.
Οι αριθμοί οι οποίοι πολλαπλασιάζονται λέγονται παράγοντες του γινομένου.
π.χ. 5 • 8 = 40
Οι δύο ιδιότητες της πρόσθεσης ισχύουν και στον πολλαπλασιασμό των φυσικών και των δεκαδικών αριθμών: Η αντιμεταθετική ιδιότητα, η προσεταιριστική ιδιότητα.
Όμως στον πολλαπλασιασμό ισχύει ακόμη μια ιδιότητα, η επιμεριστική.
Θεωρία
Διαίρεση είναι η πράξη με την οποία χωρίζουμε – μοιράζουμε έναν αριθμό σε ίσα μέρη, τόσα όσα μας λέει ένας άλλος αριθμός.
Κάνουμε διαίρεση όταν θέλουμε να μοιράσουμε (διαίρεση μερισμού) ή όταν θέλουμε να μετρήσουμε (διαίρεση μέτρησης).
- Διαίρεση μερισμού. Όταν ξέρουμε την τιμή των πολλών μονάδων και ζητάμε να βρούμε την τιμή της μιας μονάδας ( μοιράζω ένα ποσό σε ίσα μέρη)
π.χ. Τα 5 βάζα με μέλι ζυγίζουν 10 κιλά. Πόσο ζυγίζει το ένα.
- Διαίρεση μέτρησης. Όταν ξέρουμε την τιμή των πολλών μονάδων, ξέρουμε και την τιμή της μιας μονάδας και ζητάμε να βρούμε πόσες είναι οι μονάδες (Θέλω να δω πόσες φορές χωράει μια ποσότητα σε μία άλλη)
π.χ. Έχω ένα δοχείο με 10 κιλά μέλι. γέμισα βαζάκια των 2 κιλών. Πόσα βαζάκια γέμισα;
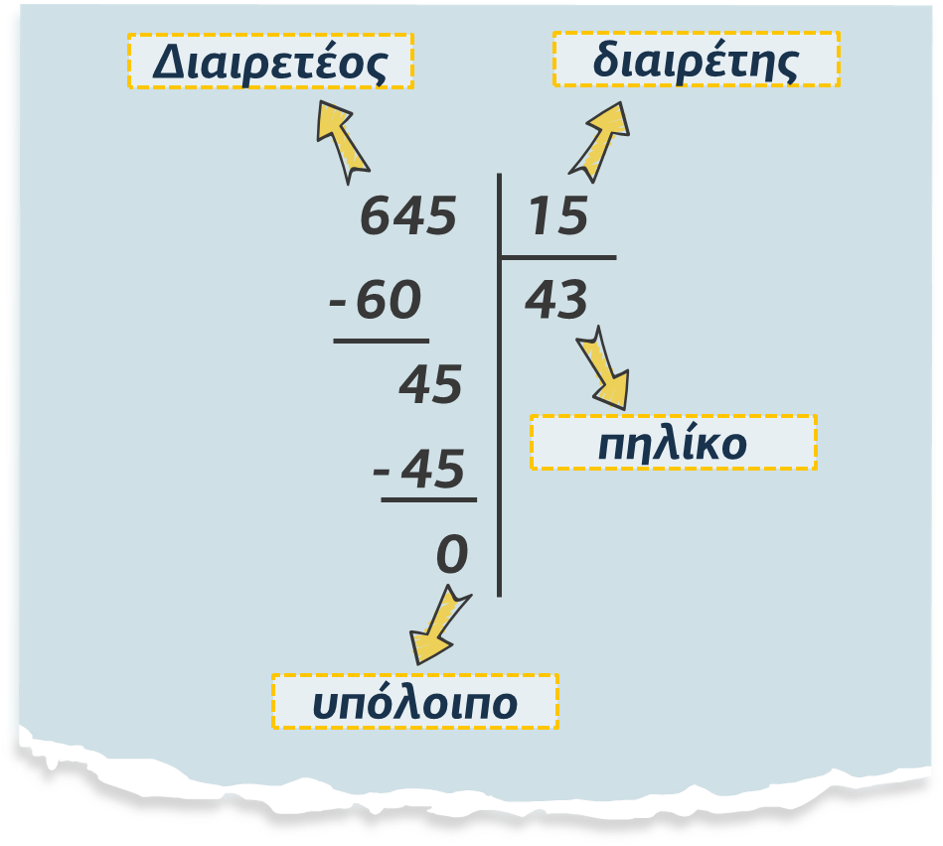 Με την πράξη της διαίρεσης έχουμε δύο φυσικούς αριθμούς Δ (Διαιρετέο) και δ (διαιρέτη) και βρίσκουμε δύο άλλους φυσικούς αριθμούς π (πηλίκο) και υ (υπόλοιπο), έτσι ώστε να ισχύει:
Με την πράξη της διαίρεσης έχουμε δύο φυσικούς αριθμούς Δ (Διαιρετέο) και δ (διαιρέτη) και βρίσκουμε δύο άλλους φυσικούς αριθμούς π (πηλίκο) και υ (υπόλοιπο), έτσι ώστε να ισχύει:
Δ = δ • π + υ
- Το υπόλοιπο είναι πάντα αριθμός μικρότερος από τον διαιρέτη και μεγαλύτερος ή ίσος του μηδενός.
- Αν το υπόλοιπο υ είναι 0, τότε έχουμε μία Τέλεια Διαίρεση: Δ = δ • π
- Η διαίρεση της μορφής Δ = δ • π + υ λέγεται Ευκλείδεια Διαίρεση.
- Κάθε αριθμός, αν διαιρεθεί με το 1, δίνει πηλίκο τον εαυτό του.
π.χ. 4 : 1 = 4
- Κάθε αριθμός, αν διαιρεθεί με τον εαυτό του, δίνει πηλίκο το 1.
π.χ. 4 : 4 = 1
- Το 0, με όποιον αριθμό και αν διαιρεθεί, δίνει πηλίκο 0.
π.χ. 0 : 1 = 0
- Ο διαιρέτης μιας διαίρεσης δεν μπορεί να είναι 0 (αδύνατη διαίρεση).
- Σε κάθε διαίρεση, αν πολλαπλασιάσω ή διαιρέσω και τους δύο όρους με τον ίδιο αριθμό, το πηλίκο δεν αλλάζει.
π.χ. 15 : 3 = 5 και (15 • 2) : (3 • 2) = 30 : 6 = 5
Θεωρία
Αριθμητική παράσταση ονομάζω μια σειρά αριθμών που συνδέονται μεταξύ τους με τα σύμβολα των πράξεων (+, –, •, :).
π.χ. 7 + 12 : 3 – 5 • ( 8 – 6 ) - 2
- Οι πράξεις σε μια αριθμητική παράσταση γίνονται από αριστερά προς τα δεξιά:
- Πρώτα γίνονται οι πολλαπλασιασμοί και οι διαιρέσεις.
- Ακολουθούν οι προσθέσεις και οι αφαιρέσεις.
- Αν υπάρχουν παρενθέσεις πρώτα γίνονται οι πράξεις μέσα στις παρενθέσεις με την ίδια σειρά (πρώτα πολλαπλασιασμοί και διαιρέσεις και μετά προσθέσεις και αφαιρέσεις).
- Αν έχουμε συνεχόμενους πολλαπλασιασμούς και διαιρέσεις ή συνεχόμενες προσθέσεις και αφαιρέσεις, οι πράξεις γίνονται με τη σειρά που βρίσκονται στην αριθμητική παράσταση.
Θεωρία
Με τη στρογγυλοποίηση αντικαθιστώ έναν αριθμό με κάποιον κοντινό του, μικρότερο ή μεγαλύτερο, για πρακτικούς λόγους.
Ένας αριθμός μπορεί να στρογγυλοποιηθεί σε οποιοδήποτε ψηφίο του, ακέραιο ή δεκαδικό, ανάλογα με την ακρίβεια που επιθυμώ.
Στρογγυλοποιώ όταν:
• δε με ενδιαφέρει το ακριβές αποτέλεσμα αλλά η εκτίμησή του,
• θέλω να διευκολυνθώ στους υπολογισμούς μου,
• θέλω να συγκρατήσω στη μνήμη μου μεγάλους αριθμούς.
Παράδειγμα
178 ≈ 180
5,23 ≈ 5,20 ή 5,2
Θεωρία
Διαιρέτες ενός φυσικού αριθμού λέγονται οι φυσικοί αριθμοί που διαιρούν ακριβώς αυτό τον αριθμό.
Παράδειγμα
Ο αριθμός 8 έχει διαιρέτες τους αριθμούς 1, 2, 4, 8, γιατί:
8 : 1 = 8, 8 : 2 = 4, 8 : 4 = 2, 8 : 8 = 1
| Κάθε φυσικός αριθμός έχει τουλάχιστον δύο διαιρέτες: τη μονάδα και τον εαυτό του. |
| Οι διαιρέτες ενός φυσικού αριθμού είναι πάντα μικρότεροι ή ίσοι του αριθμού. π.χ. οι διαιρέτες του 12 είναι οι 1, 2, 3, 4, 6, 12. |
Μέγιστος Κοινός Διαιρέτης (Μ.Κ.Δ.) δύο ή περισσότερων φυσικών αριθμών είναι ο μεγαλύτερος από τους κοινούς διαιρέτες των αριθμών αυτών.
Παράδειγμα
οι διαιρέτες του 12 και του 38 είναι:
Δ12 = 1, 2, 3, 4, 6, 12
Δ18 = 1, 2, 3, 6, 9, 18
Κοινοί Διαιρέτες (Κ.Δ.) του 12 και 18 είναι τα 2, 3, 6.
Άρα Μέγιστος Κοινός Διαιρέτης (Μ.Κ.Δ.) = 6