-
Αριθμοί και πράξεις
Σε αυτή τη θεματική ενότητα θα ασχοληθούμε με τους αριθμούς και τις πράξεις με αριθμούς.
Θα ξεκινήσουμε από τα αριθμητικά σύμβολα τα οποία χρησιμοποιούμε από την Α΄ Δημοτικού για να φτιάξουμε τους αριθμούς και να κάνουμε υπολογισμούς.
Ξέρετε πως οι Ινδοί τα χρησιμοποιούσαν από το 350 π.X.; Γνωρίζετε ακόμα ότι τα δίδαξαν αργότερα οι Άραβες στους Ευρωπαίους και για τον λόγο αυτό ονομάστηκαν «αραβικοί αριθμοί»;
Τα σύμβολα που γνωρίζουμε δεν τελειοποιήθηκαν σε κάποιον ορισμένο χρόνο ή τόπο αλλά εξελίχτηκαν με συνεχή ανάπτυξη και πιθανότατα τελειοποιήθηκαν τους τελευταίους αιώνες.
Στο σκίτσο που ακολουθεί βλέπετε την εξέλιξη των συμβόλων από το 800 μετά Χριστόν έως σήμερα.
Τι θα μάθουμε σε αυτή την ενότητα:
14. Πρώτοι και σύνθετοι αριθμοί
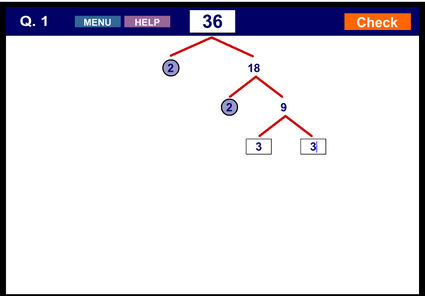
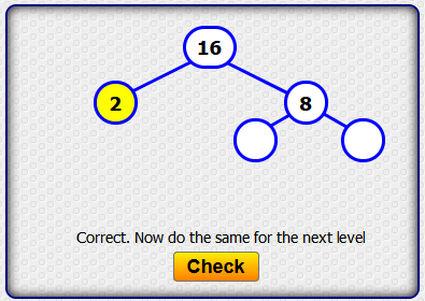
15. Παραγοντοποίηση φυσικών αριθμών
16. Πολλαπλάσια ενός αριθμού - Ε.Κ.Π
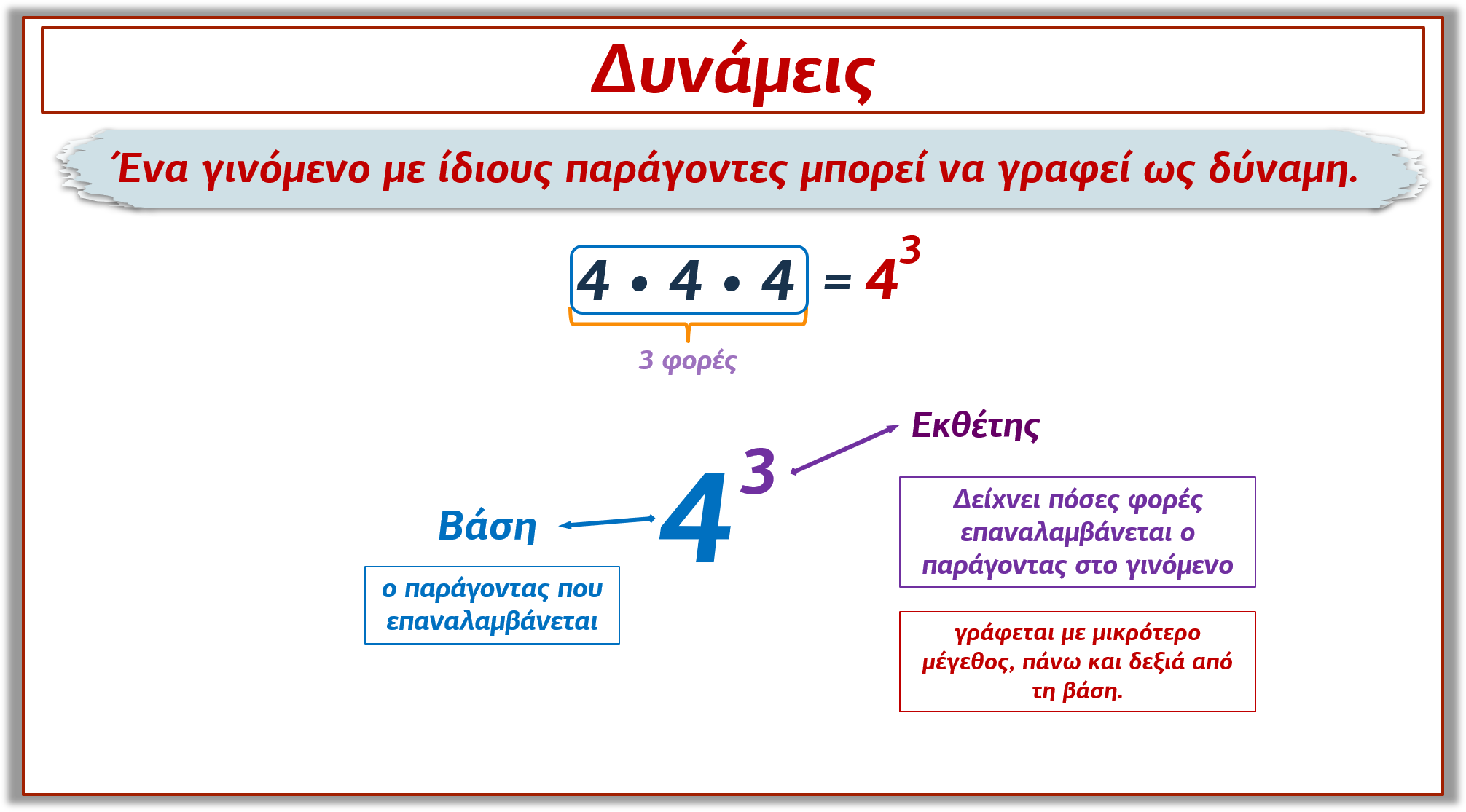
17. Δυνάμεις - Δυνάμεις του 10
19. Κλάσματα ομώνυμα και ετερώνυμα
20. Το κλάσμα ως ακριβές πηλίκο διαίρεσης
21. Ισοδύναμα κλάσματα
22. Σύγκριση - Διάταξη κλασμάτων
23. Προβλήματα με πρόσθεση και αφαίρεση κλασμάτων
24. Προβλήματα με πολλαπλασιασμό και διαίρεση κλασμάτων
Θεωρία
Το κόσκινο του Ερατοσθένη
Η εύρεση των πρώτων αριθμών απασχόλησε από την αρχαιότητα τους μαθηματικούς. Ένας από τους πιο απλούς αλλά και αργούς τρόπους για (μαζική) εύρεση πολλών πρώτων είναι το λεγόμενο κόσκινο του Ερατοσθένη. Μπορούμε να βρούμε όλους τους πρώτους αριθμούς μέχρι το 100 (ή μέχρι οποιονδήποτε δοσμένο αριθμό). Στον διπλανό πίνακα διαγράφουμε το 1 που δεν είναι πρώτος ούτε σύνθετος. Κυκλώνουμε το 2 και διαγράφουμε όλα τα πολλαπλάσιά του. Ο επόμενος αριθμός που συναντάμε (χωρίς να έχει σβηστεί) είναι πρώτος. Επαναλαμβάνουμε τη διαδικασία με το 3, το 5 και το 7. Με αυτό τον τρόπο διαγράφονται όλοι οι σύνθετοι αριθμοί και μένουν μόνο οι πρώτοι από το 1 έως το 100.
Θεωρία
Πολλαπλάσιο (Π) ενός φυσικού αριθμού λέγεται ο αριθμός που προκύπτει όταν τον πολλαπλασιάσουμε με έναν άλλο φυσικό αριθμό (0, 1, 2, 3, 4, 5, . . .)
Παράδειγμα
Τα πολλαπλάσια του 2 και του 3
Π2 = 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, …
Π3 = 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …
| Κάθε φυσικός αριθμός έχει άπειρα πολλαπλάσια γιατί είναι και άπειροι οι αριθμοί με τους οποίους μπορώ να τον πολλαπλασιάσω |
Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) δύο ή περισσότερων φυσικών αριθμών λέγεται το μικρότερο από τα κοινά πολλαπλάσιά τους, εκτός από το 0.
Παράδειγμα
Τα πολλαπλάσια του 2 και του 3 είναι:
Π2 = 0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, …
Π3 = 0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, …
Κοινά Πολλαπλάσια (Κ.Π.) του 2 και 3 είναι τα 6, 12, 18, 24.
Άρα το Ελάχιστο Κοινό Πολλαπλάσιο (Ε.Κ.Π.) = 6
Θεωρία
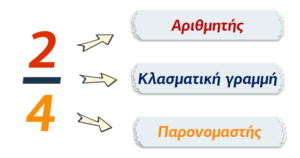
- Ο παρονομαστής μας δείχνει σε πόσα ίσα μέρη έχουμε χωρίσει την ακέραιη μονάδα.
- Ο αριθμητής μας δείχνει πόσα από τα ίσα μέρη, στα οποία χωρίστηκε η ακέραια μονάδα, πήραμε.
- Η κλασματική γραμμή είναι η πράξη της διαίρεσης.
- Κάθε κλάσμα μας εκφράζει το μέρος του ολόκληρου (αριθμητής το μέρος, παρονομαστής το ολόκληρο)
Κλασματική μονάδα είναι το ένα από τα ίσα μέρη που χωρίσαμε την ακέραιη μονάδα.
Είναι ένα κλάσμα που έχει αριθμητή την μονάδα (1).
Κλασματική μονάδα μπορεί να είναι και το ένα από τα ίσα μέρη, στα οποία χωρίζουμε ένα πλήθος ομοειδών αντικειμένων. Π.χ. το 1/5 των 20 μαθητών.
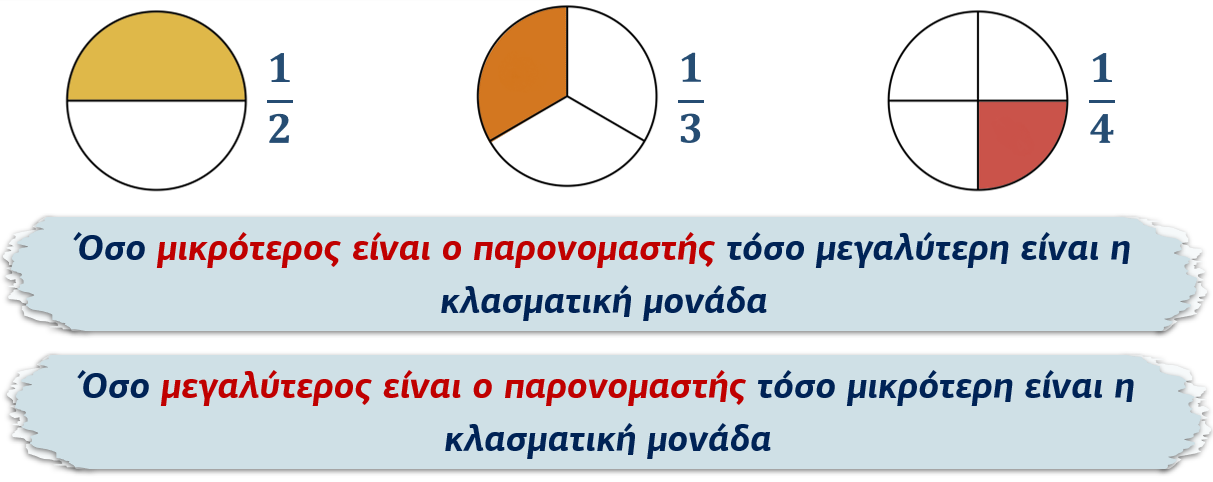
Ανάμεσα σε δύο ή περισσότερες κλασματικές μονάδες μεγαλύτερη είναι εκείνη που έχει το μικρότερο παρονομαστή και μικρότερη εκείνη που έχει το μεγαλύτερο παρονομαστή.
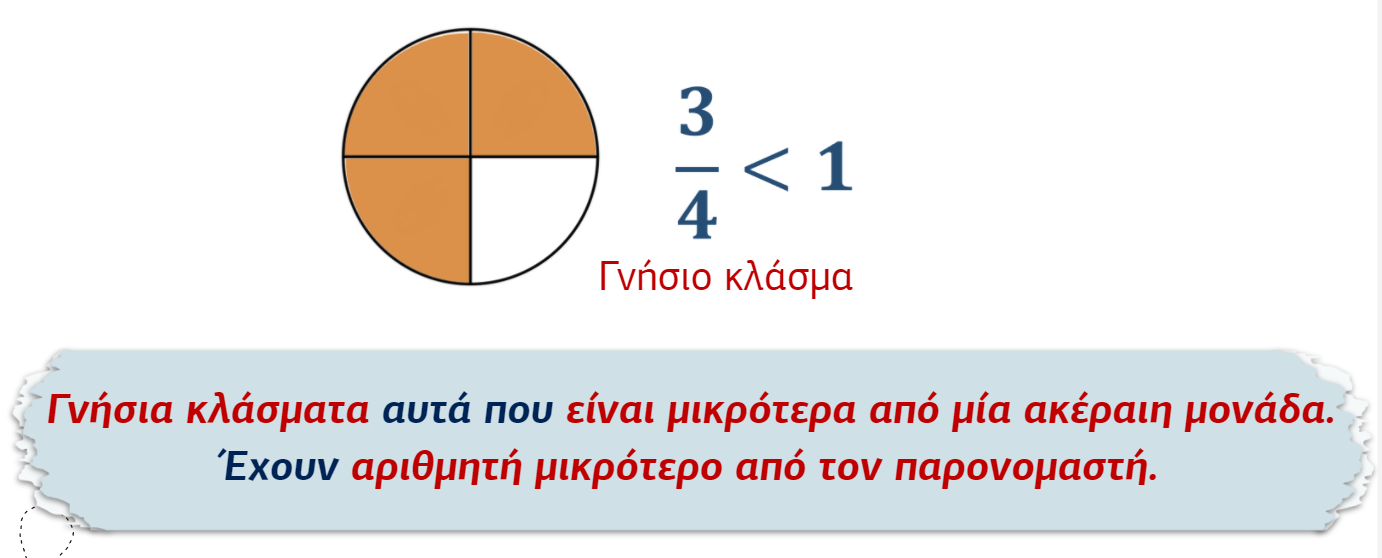
Γνήσια κλάσματα
• Τα κλάσματα που έχουν αριθμητή μικρότερο από τον παρονομαστή λέγονται γνήσια κλάσματα. Αυτά είναι μικρότερα από μία ακέραιη μονάδα.
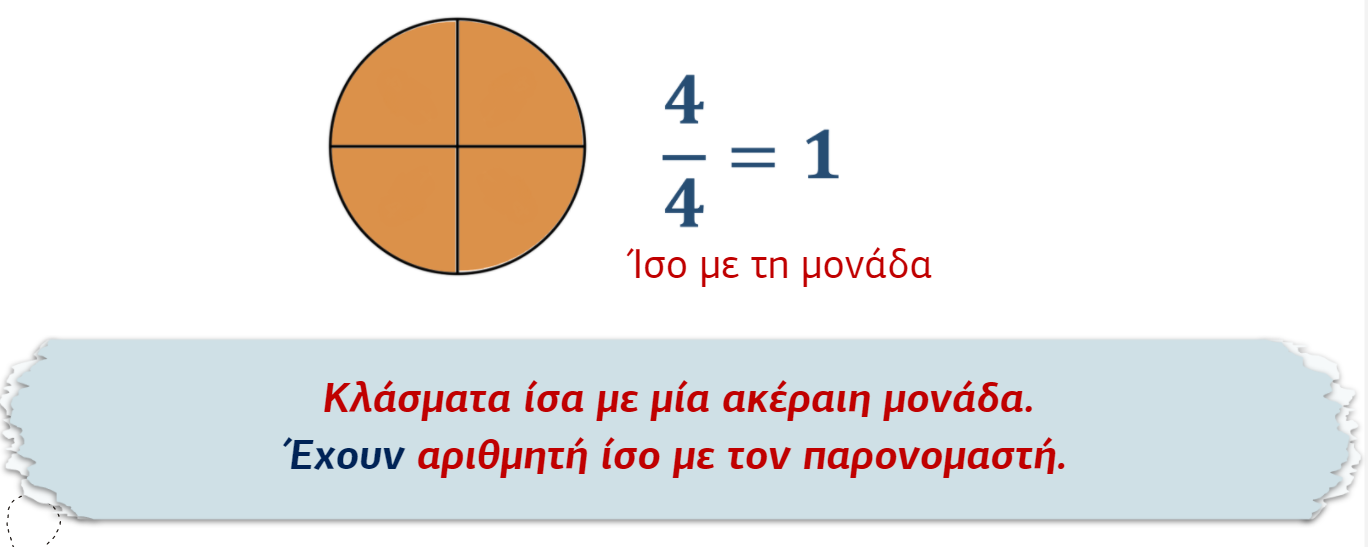
Ίσα με την ακέραιη μονάδα
• Τα κλάσματα που έχουν αριθμητή ίσο με τον παρονομαστή λέγονται ισοδύναμα (ίσα) με την ακέραιη μονάδα. Αυτά έχουν την ίδια αξία με την ακέραιη μονάδα.
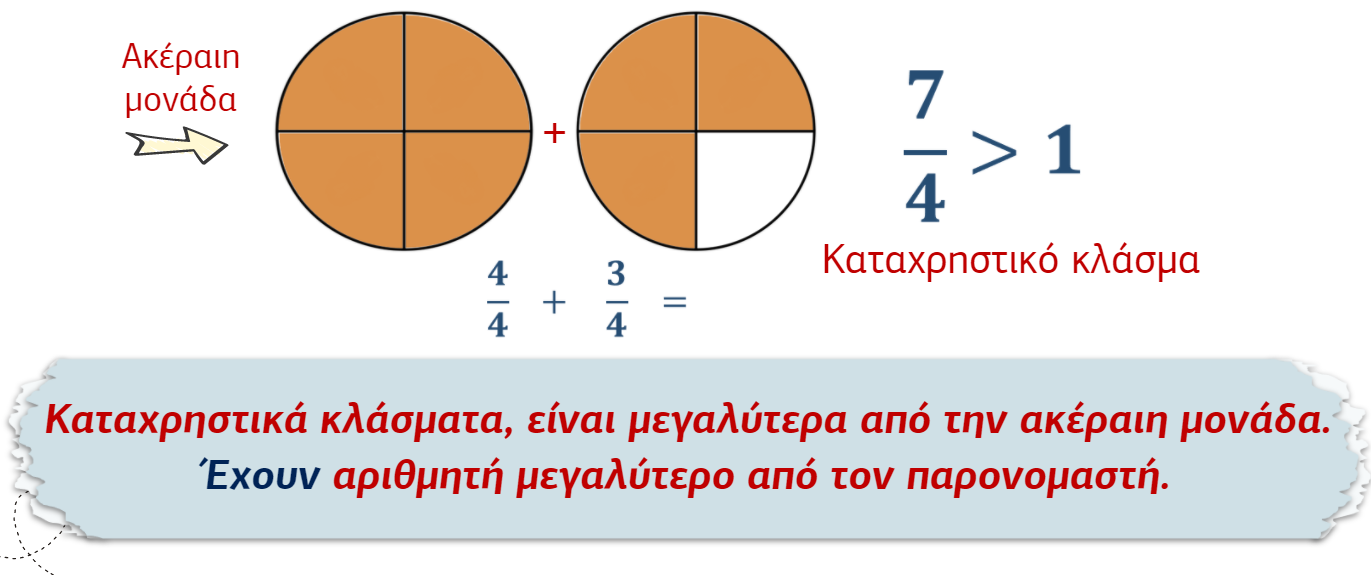
Καταχρηστικά κλάσματα
• Τα κλάσματα που έχουν αριθμητή μεγαλύτερο από τον παρονομαστή λέγονται καταχρηστικά κλάσματα. Αυτά είναι μεγαλύτερα από μία ακέραιη μονάδα.
Δραστηριότητες
Μαθαίνω παίζοντας
Θεωρία
- Κάθε κλάσμα είναι ίσο με το πηλίκο μιας διαίρεσης: (αριθμητής) : (παρονομαστή)
- Αντίστροφα κάθε διαίρεση μπορούμε να την εκφράσουμε και ως κλάσμα.
- Κάθε κλάσμα μπορεί να εκφραστεί ως δεκαδικός αν κάνουμε τη διαίρεση.
- Αν η διαίρεση είναι ατελής σταματάμε όπου μας χρειάζεται.
- Κάθε δεκαδικός μπορεί να μετατραπεί σε κλάσμα.
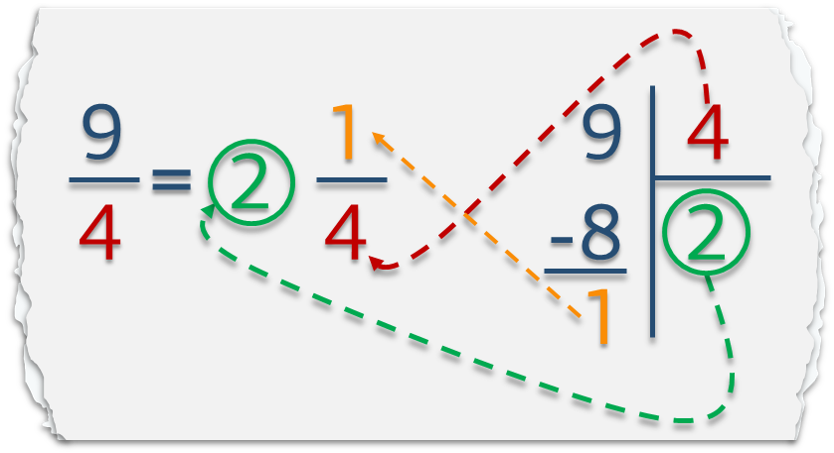
- Κάθε καταχρηστικό κλάσμα μπορώ να το μετατρέψω σε μεικτό με τη διαίρεση (αριθμητής : παρονομαστή)
Θεωρία
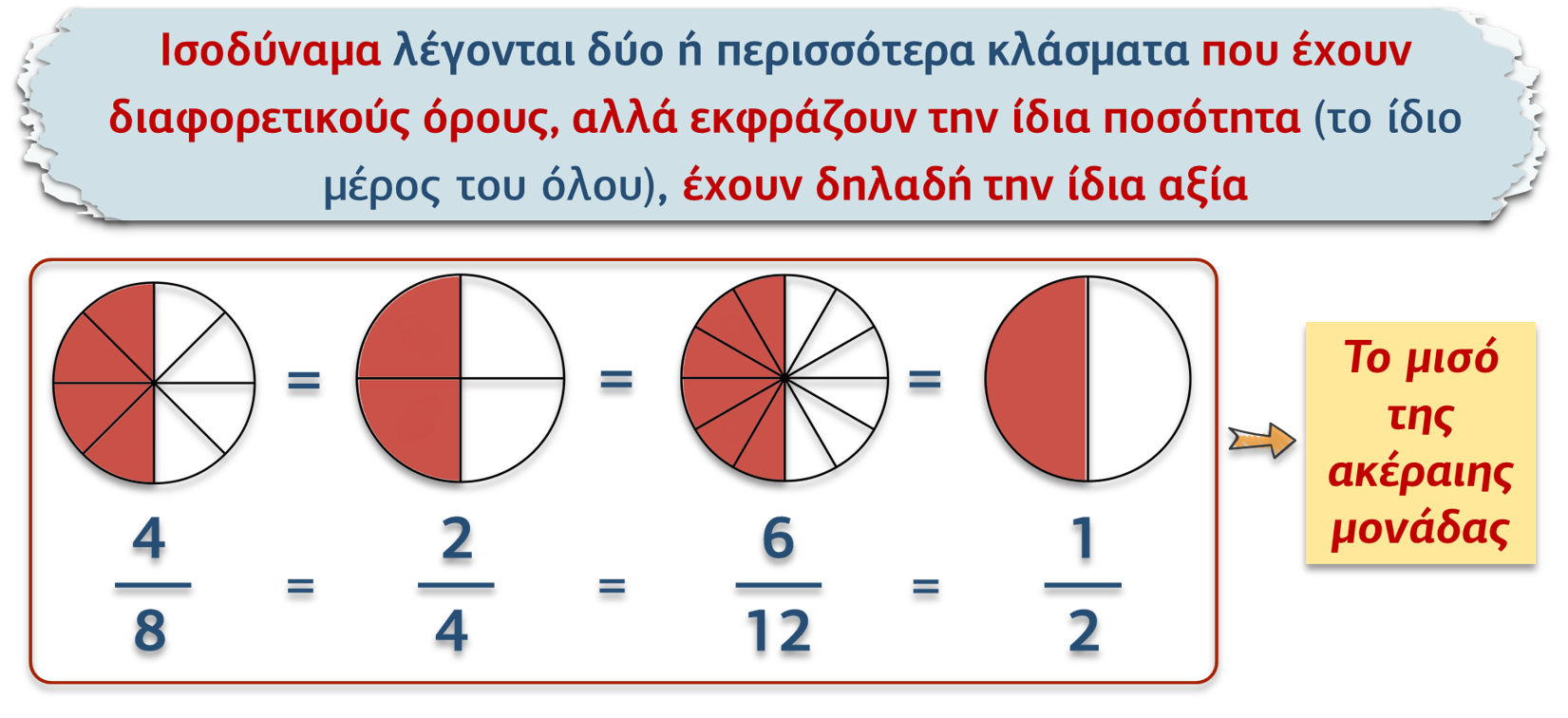
Δύο ή περισσότερα κλάσματα που έχουν διαφορετικούς όρους, δηλαδή διαφορετικό αριθμητή & παρονομαστή, αλλά εκφράζουν την ίδια ποσότητα, λέγονται ισοδύναμα.
Δημιουργώ ισοδύναμα κλάσματα πολλαπλασιάζοντας ή διαιρώντας και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό.
Όταν πολλαπλασιάζω και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό, προκύπτει ένα κλάσμα ισοδύναμο με το αρχικό με μεγαλύτερους όρους
Όταν διαιρώ και τους δύο όρους ενός κλάσματος με τον ίδιο αριθμό, προκύπτει ένα κλάσμα ισοδύναμο με το αρχικό με μικρότερους όρους
Απλοποίηση ενός κλάσματος λέγεται η εύρεση ενός ισοδύναμου κλάσματος με μικρότερους όρους. Αυτό γίνεται διαιρώντας τους δυο όρους του αρχικού κλάσματος με τον ίδιο αριθμό.
Προσέχω! Διαιρώ κάθε φορά με τους Κ.Δ του αριθμητή και του παρονομαστή, το αρχικό κλάσμα.
Αν ένα κλάσμα δεν μπορεί να απλοποιηθεί (δεν υπάρχει αριθμός εκτός από το 1, που να είναι κοινός διαιρέτης του αριθμητή και του παρονομαστή του), ονομάζεται ανάγωγο.
Μαθαίνω παίζοντας
Θεωρία
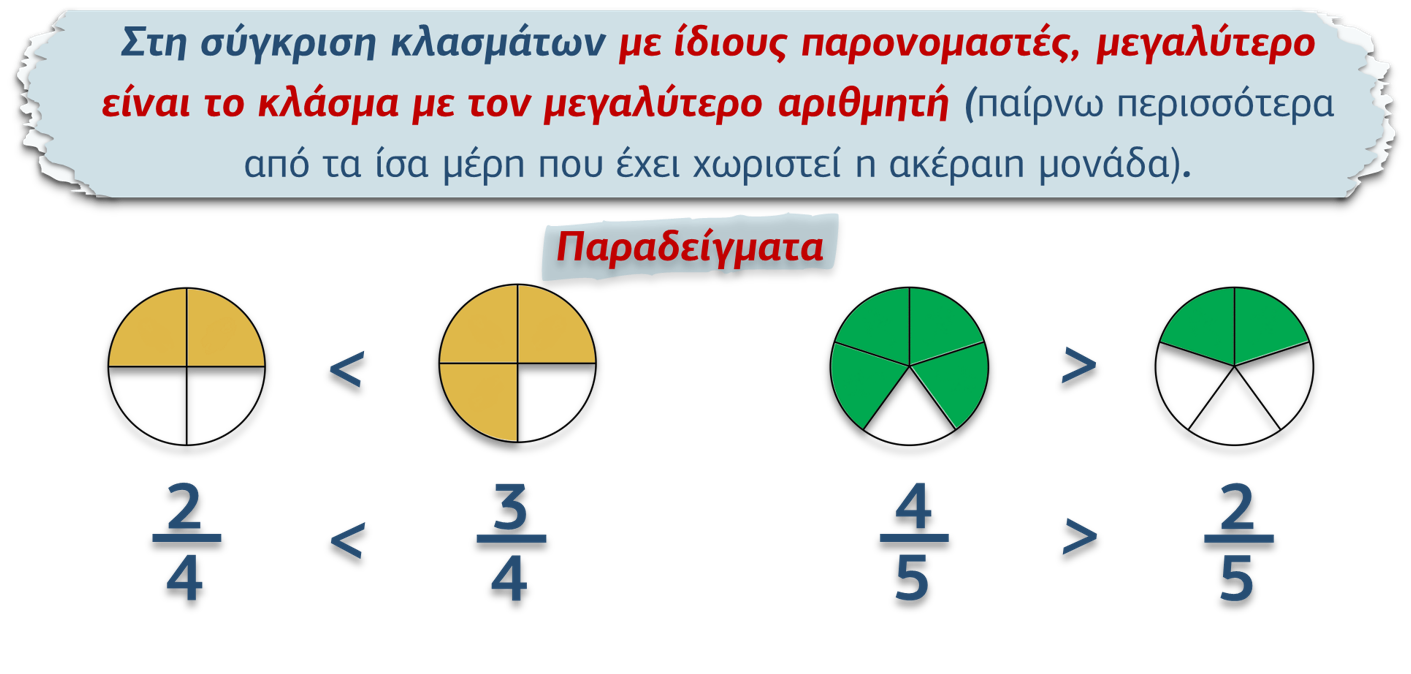
• Στη σύγκριση δύο ή περισσότερων κλασμάτων, μεγαλύτερο είναι το κλάσμα που εκφράζει μεγαλύτερο μέρος του όλου (της ακέραιης μονάδας).
• Στη σύγκριση κλασμάτων με ίδιους παρονομαστές, μεγαλύτερο είναι το κλάσμα με τον μεγαλύτερο αριθμητή (παίρνω περισσότερα από τα ίσα μέρη που έχει χωριστεί η ακέραιη μονάδα).
• Στη σύγκριση κλασμάτων με ίδιους αριθμητές, μεγαλύτερο είναι το κλάσμα με τον μικρότερο παρονομαστή, επειδή παίρνω ίδιο αριθμό μερών, αλλά κάθε μέρος είναι μεγαλύτερο σε μέγεθος (η ακέραιη μονάδα έχει χωριστεί σε λιγότερα μέρη).
Θεωρία
Προσθέτω - Αφαιρώ ομώνυμα κλάσματα
• Για να προσθέσω ομώνυμα κλάσματα, προσθέτω τους αριθμητές τους και αφήνω τον ίδιο παρονομαστή
• Για να αφαιρέσω ομώνυμα κλάσματα, αφαιρώ τους αριθμητές και αφήνω τον ίδιο παρονομαστή
Προσθέτω - Αφαιρώ ετερώνυμα κλάσματα
• Για να προσθέσω ετερώνυμα κλάσματα, τα μετατρέπω πρώτα σε ομώνυμα και μετά κάνω την πρόσθεση
• Για να αφαιρέσω ετερώνυμα κλάσματα, τα μετατρέπω πρώτα σε ομώνυμα και μετά κάνω την αφαίρεση
Μαθαίνω παίζοντας
Θεωρία
• Στον πολλαπλασιασμό δεν εξετάζω αν τα κλάσματα είναι ομώνυμα ή ετερώνυμα.
• Για να πολλαπλασιάσω κλάσματα πολλαπλασιάζω αριθμητή με αριθμητή και παρονομαστή με παρονομαστή.
• Για να πολλαπλασιάσω κλάσμα με ακέραιο ή ακέραιο με κλάσμα μετατρέπω τον ακέραιο σε κλάσμα και στην συνέχεια πολλαπλασιάζω τα κλάσματα
• Στην διαίρεση δεν εξετάζω αν τα κλάσματα είναι ομώνυμα ή ετερώνυμα.
• Για να διαιρέσω κλάσματα αντιστρέφω το δεύτερο κλάσμα και μετά πολλαπλασιάζω αριθμητή με αριθμητή και παρονομαστή με παρονομαστή.
• Για να διαιρέσω κλάσμα με ακέραιο ή ακέραιο με κλάσμα μετατρέπω τον ακέραιο σε κλάσμα και στην συνέχεια κάνω την διαίρεση.